Сколько же дифирамбов спето в сети интернет про графики ренко, их грандиозные преимущества перед стандартными графиками за счет отвязки от временного интервала. А так ли это на самом деле? Так ли плохо знать сколько времени формировался каждый ренко-кирпичик?
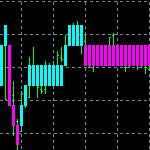
Давайте попробуем разобраться в указанных преимуществах. Так, к примеру, выглядит «стандартный» график ренко.
А вот так выглядит график, построенный по принципу ренко, но учитывающий время формирование каждого бара.
Обратите внимание, насколько продолжительными по времени являются отдельные бары. А не те ли это самые уровни поддержки и сопротивления, о которых так же пестрят страницы интернет, но нигде не описано принципов определения этих самых уровней? А вот так это выглядит в динамике.
Сказать по чести — я еще не решил для себя что делать с этими затяжными барами, какие сигналы по ним формировать. Но работа в данном направлении ведется. В конце повествования приведу исходный код индикатора, примеры которого опубликованы на виде и скриншоте.
#property copyright "2017, SergDeev"
#property link "http://fx-prog.ru"
#property description "RenkoTimes"
#property version "1.0"
#property strict
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_color1 clrMagenta
#property indicator_color2 clrAqua
#property indicator_width1 2
#property indicator_width2 2
extern int RenkoPoint=10;
extern int CountBars=0;
double Bear_Buffer[],Bull_Buffer[];
int OnInit(void) {
IndicatorDigits(Digits);
SetIndexStyle(0,DRAW_HISTOGRAM); SetIndexBuffer(0,Bear_Buffer); SetIndexLabel(0,"Bear");
SetIndexStyle(1,DRAW_HISTOGRAM); SetIndexBuffer(1,Bull_Buffer); SetIndexLabel(1,"Bull");
if(Digits==5 || Digits==3) RenkoPoint *= 10;
if (CountBars == 0) CountBars = (int)ChartGetInteger(0,CHART_WIDTH_IN_BARS);
return(INIT_SUCCEEDED);
}
int start() {
int i,limit;
int counted_bars=IndicatorCounted();
if (counted_bars>0) counted_bars--;
limit=Bars-counted_bars;
if (limit > CountBars) limit = CountBars;
else if (limit>0) limit--;
if (counted_bars == 0) {
if (Close[limit]>Open[limit]) {
Bull_Buffer[limit]=High[limit];
Bear_Buffer[limit]=NormalizeDouble(Bull_Buffer[limit]-RenkoPoint*Point,Digits);
}
else {
Bull_Buffer[limit]=Low[limit];
Bear_Buffer[limit]=NormalizeDouble(Bull_Buffer[limit]+RenkoPoint*Point,Digits);
}
limit--;
}
for (i=limit; i>=0; i--) {
double min = MathMin(Bear_Buffer[i+1],Bull_Buffer[i+1]);
double max = MathMax(Bear_Buffer[i+1],Bull_Buffer[i+1]);
int x=1;
while (High[i] >= (max+x*RenkoPoint*Point)) {
Bull_Buffer[i] = NormalizeDouble(max+x*RenkoPoint*Point,Digits);
Bear_Buffer[i] = max;
x++;
}
x=1;
while (Low[i] <= (min-x*RenkoPoint*Point)) {
Bull_Buffer[i] = NormalizeDouble(min-x*RenkoPoint*Point,Digits);
Bear_Buffer[i] = min;
x++;
}
if (Bear_Buffer[i] == EMPTY_VALUE || Bull_Buffer[i] == EMPTY_VALUE) {
if (Bear_Buffer[i+1] > Bull_Buffer[i+1]) {
Bull_Buffer[i] = Bull_Buffer[i+1];
Bear_Buffer[i] = Bull_Buffer[i]+RenkoPoint*Point;
}
else if (Bull_Buffer[i+1] > Bear_Buffer[i+1]) {
Bull_Buffer[i] = Bull_Buffer[i+1];
Bear_Buffer[i] = Bull_Buffer[i]-RenkoPoint*Point;
}
}
}
return(0);
}

 2 мая, 2017
2 мая, 2017 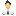 Sergey
Sergey 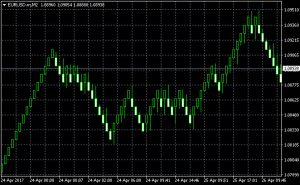
 Опубликовано в рубрике
Опубликовано в рубрике  Теги:
Теги: 

